Do you know what really charges me up? Discussing protein electrostatics, of course!
Proteins are made up of amino acids. A few amino acids are positively charged at biologically relevant pH values, and a few others are negatively charged. The number of charged amino acids in a protein and where those charges are located on a protein’s structure are both really important for how that protein interacts with other biomolecules and its overall function.
In protein purification, we leverage this intrinsic protein feature – its charge at a given pH value – to help purify that protein. Protein charge is especially relevant to ion-exchange chromatography. To perform ion-exchange chromatography, however, it helps to know what a protein’s charge is and how that charge varies with pH.
A protein’s net charge depends on the pH and the pKa values of the ionizable groups within that protein. A protein will be net neutral when the pH is equal to its isoelectric point (pI), positive at pH values more acidic than its pI, and negative at pH values more basic than its pI.
In this article we will discuss the chemical basics of protein charge and cover conceptual and quantitative ways to approach this fundamental property of proteins.
In this article:
Estimating Protein Charge for Protein Purification
Calculating Protein Isoelectric Point
Acids and Bases
First, we need to review some chemistry basics regarding acids and bases.
In chemistry terms, an acid is a moiety that donates a hydrogen atom (H+), also known as a proton, to a chemical reaction. On the other side of the chemical reaction, a base accepts the hydrogen atom.
For example, when hydrochloric acid (HCl) and sodium hydroxide (NaOH) react, they form salt (NaCl) and water (H2O) (Equation 1). In this reaction, HCl is the acid that donates a hydrogen atom, and the basic hydroxide accepts the hydrogen atom to form water.
Equation 1. Acid-base reaction of hydrochloric acid (HCl) and sodium hydroxide (NaOH).
An important term we need to talk about is the acid dissociation constant (Ka). The Ka for an acid is the ratio of the concentrations of the conjugate base and hydrogen versus the concentration of the protonated acid in solution (Equation 2). That is a mouthful!
Let’s use Equation 2 and the examples of HCl and NaOH to walk through this math and explain what Ka really means.
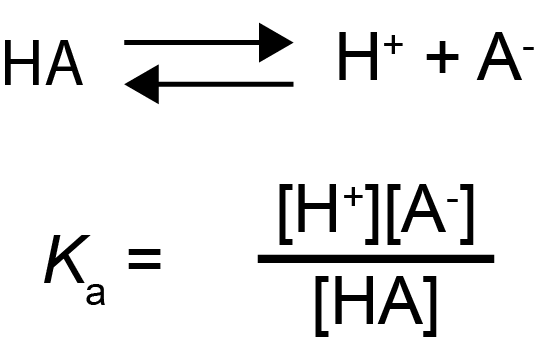
Equation 2. A generic acid dissociation equation is denoted by the acid (HA) dissociating into a hydrogen atom (H+) and a conjugate base (A-) (top). The acid dissociation constant is the product of H+ and A- concentrations divided by the concentration of HA (bottom).
HCl readily dissolves into H+ and Cl- in solution, making the H+ available for chemical reactions. Since H+ and Cl- concentrations are high, and the concentration of HCl is low, HCl has a high acid dissociation constant - that is why HCl is a strong acid!
Another way of saying that NaOH is a strong base is to say that it is a very poor acid. The hydroxide will only give up its H+ when interacting with an even stronger base, such as alkane (pKa > 50) for example.
When talking about acids and bases in protein biochemistry,
we usually do not directly refer to
Ka values. Instead, we
mention the related p
Ka value. The pKa is
the negative log of the dissociation constant (Equation 3). p
Ka
values range between -10 and 50. Lower values, including negative values,
indicate a strong acid. And higher values indicate a strong base. HCl and NaOH,
for example, have p
Ka values of -6 and 15, respectively.
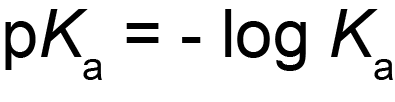
If you want to learn even more about acids, bases and pKa, this article walks you through a lot!
Amino Acids and Bases
Ok – back to proteins! What are the relevant acids and bases in proteins?
The main acids are carboxy groups, and there are a few different main bases including amino groups (Figure 1). Carboxy groups are also known as carboxyl groups. While both terms mean the same thing, I’ll use the former term here because that’s what’s ingrained in my head.
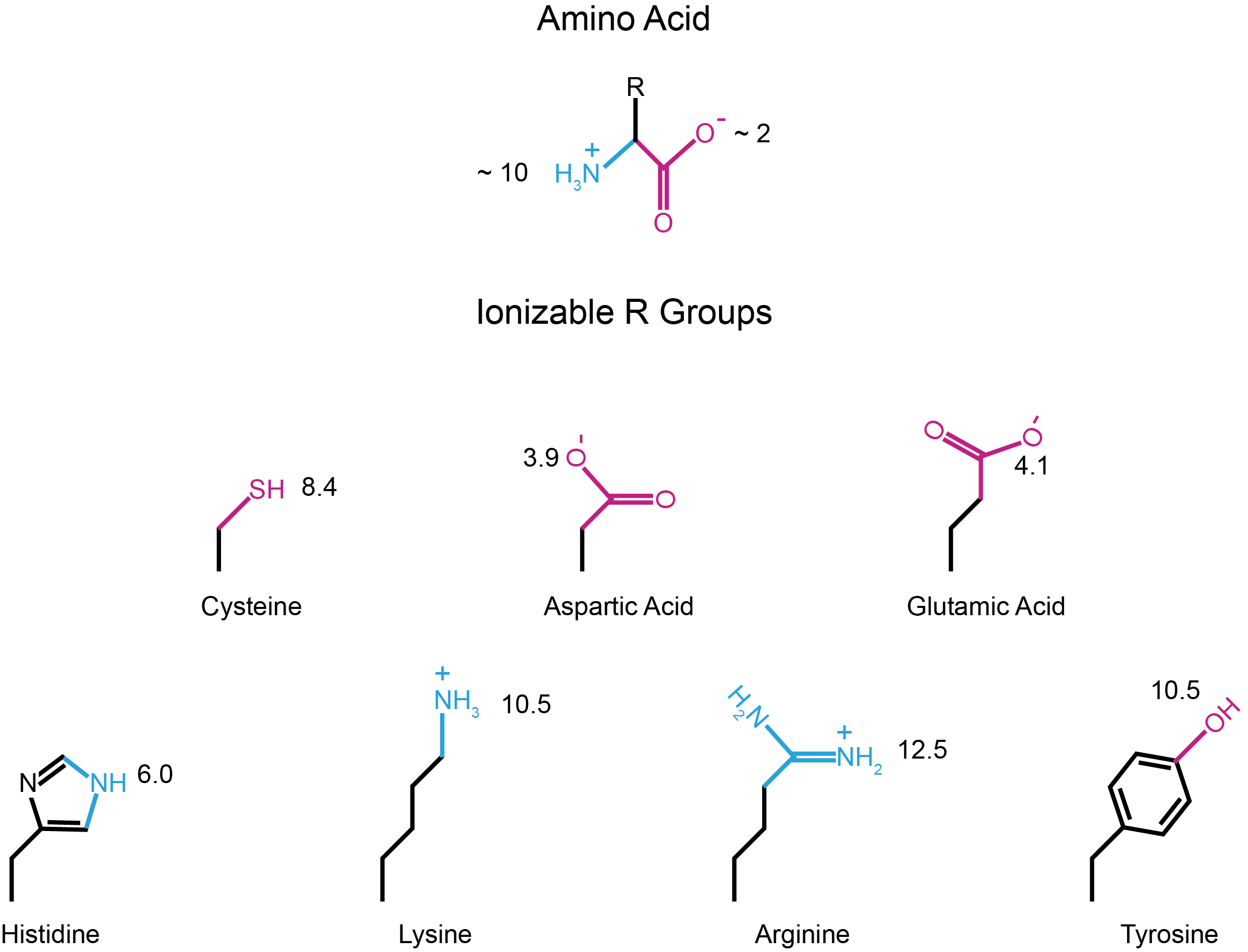
Figure 1. pKa
values of amino acid amino and carboxy groups (top), and ionizable R groups
(bottom). Groups that can be negative, including carboxy groups, are colored
magenta. Groups that can be positive, including amino groups, are colored blue.
Every amino acid, by itself, has an amino (N) and a carboxy (C) group. Amino and carboxy groups have pKa values of ~10 and ~2, respectively. This means at neutral pH 7, amino groups will be positively charged and carboxy groups will be negatively charged. Note that the exact pKa values of these groups varies a little bit depending on which amino acid you are considering (Table 1).
However, to form a protein, adjacent amino acids use their carboxy and amino groups to form a peptide bond (Figure 2). Peptide bond formation neutralizes the charge of these groups so that a protein will only have one positive charge on the amino group of the first amino acid and only one negative charge on the carboxy group of the last amino acid.
Therefore, most of a protein’s charge will come from the side chains (R) of its constituent amino acids.
Carboxy side chains in glutamic acid and aspartic acid have pKa values of ~ 4, making them negative under most biological pH conditions.
The side chains of arginine, lysine, and tyrosine possess moieties with basic pKa values, meaning that these side chains will be protonated in most biological pH conditions.
The side chains of cysteine and histidine have pKa values within the biologically relevant pH range (~4.5 to 8.5), meaning that these side chains can be either charged or neutral, depending on the surrounding pH environment (Figure 1).
Table 1. pKa values for free amino acid ionizable groups.
|
Amino Acid |
pKa values |
||
|
Amino (N) |
Carboxy (C) |
Side Chain (R) |
|
|
Alanine (A) |
9.9 |
2.4 |
- |
|
Cysteine (C) |
10.7 |
1.9 |
8.4 |
|
Aspartic Acid (D) |
9.9 |
2.0 |
3.9 |
|
Glutamic Acid (E) |
9.5 |
2.1 |
4.1 |
|
Phenylalanine (F) |
9.3 |
2.2 |
- |
|
Glycine (G) |
9.8 |
2.4 |
- |
|
Histidine (H) |
9.3 |
1.8 |
6.0 |
|
Isoleucine (I) |
9.8 |
2.3 |
- |
|
Lysine (K) |
9.1 |
2.2 |
10.5 |
|
Leucine (L) |
9.7 |
2.3 |
- |
|
Methionine (M) |
9.3 |
2.1 |
- |
|
Asparagine (N) |
8.7 |
2.1 |
- |
|
Proline (P) |
10.6 |
2.0 |
- |
|
Glutamine (Q) |
9.1 |
2.2 |
- |
|
Arginine (R) |
9.0 |
1.8 |
12.5 |
|
Serine (S) |
9.2 |
2.2 |
- |
|
Threonine (T) |
9.1 |
2.1 |
- |
|
Valine (V) |
9.7 |
2.3 |
- |
|
Tryptophan (W) |
9.4 |
2.5 |
- |
|
Tyrosine (Y) |
9.2 |
2.2 |
10.5 |
Values from Carmelo Rizzo of Vanderbilt University (Rizzo, n.d.)
Figure 2. Charges on the amino and carboxy groups are neutralized in peptide bond formation.
Protein Charge
Considering all of the pKa values for a given protein will yield what is known as that protein’s isoelectric point (pI). Conceptually, the isoelectric point is the pH at which a protein will be net neutral or chargeless. So, let’s say we’ve determined the isoelectric point for a protein is 7 (pI of 7) then when it is in a buffer with a pH of 7, your protein will be net neutral or chargeless.
Now there will likely still be charges on the protein at its isoelectric point, but an equal number of positive and negative charges that will balance out to make the overall protein charge zero (Figure 3).
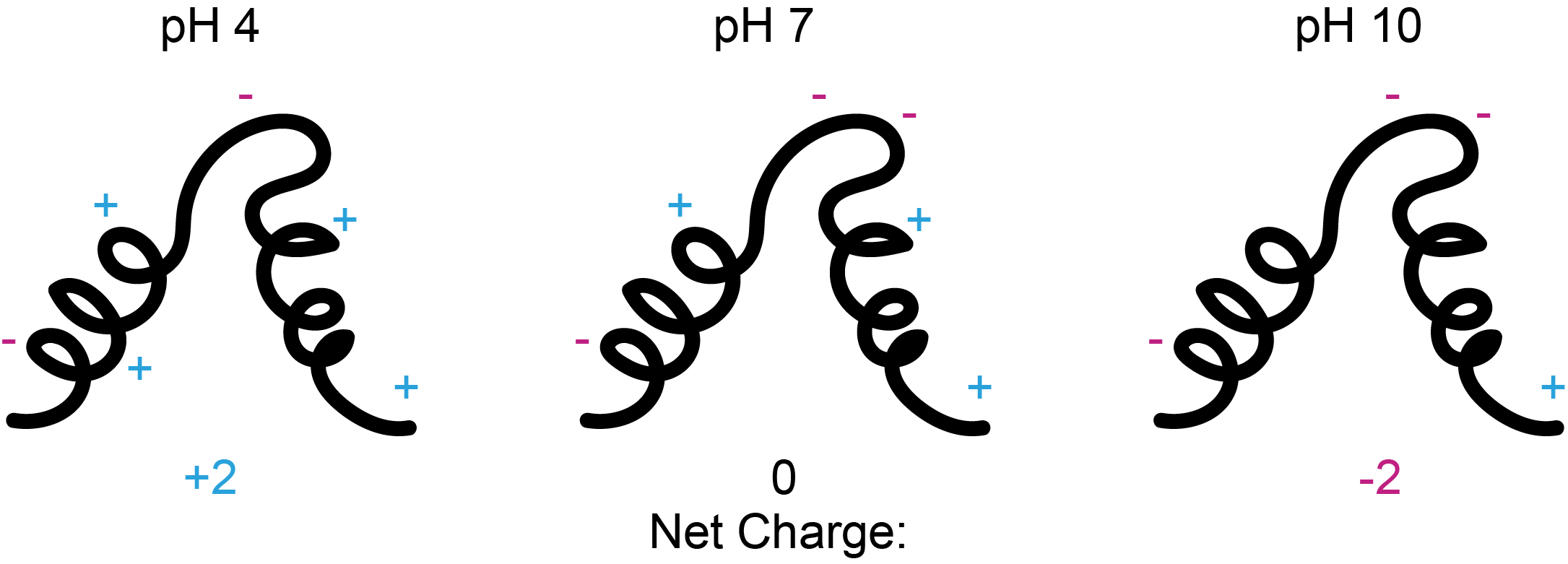
Figure 3. A protein with an isoelectric point (pI) of 7 will have a net charge of 0 at pH 7 (center). At more acidic pH values, it will be positively charged (left) and at more basic pH values it will be negatively charged (right).
This framing of the isoelectric point also helps us qualitatively determine a protein’s charge at a given pH. Remember that pH is also a log-based scale with values between 0 and 14. pH is the negative log of the concentration of hydrogen atoms in a solution (Equation 3). A pH of 7 is considered neutral, and similar to the pKa scale, lower values are acidic and higher values are basic.
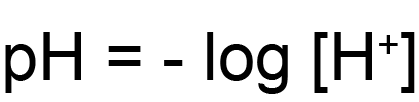
Equation 4. pH is the negative log of the hydrogen ion concentration in a solution.
Estimating Protein Charge for Protein Purification
Ok, let’s go over an example to cover how we might practically apply this math in the lab. For this example, let’s pretend that we are purifying a protein with an isoelectric point (pI) of 7.
If we use a protein purification buffer with a pH of 7, the net charge will be zero and our protein likely won’t stick to cation-exchange nor anion-exchange columns (Figure 4). So, pH 7 would be a poor choice if we are trying to purify this protein using ion-exchange chromatography.
Figure 4. A protein with a pI of 7 likely won’t bind to cation or anion exchange columns at pH 7 (left). However, it will be positively charged at pH 4 and bind to an anion exchange column (middle), and it will be negatively charged at pH 10 and will bind to a cation exchange column (right).
Instead, let’s try an acidic buffer with pH 4. A buffer with pH 4 will have a higher concentration of hydrogen atoms in solution compared to pH 7 where our hypothetical protein is neutral. The increased concentration of H+ will lead to the protonation of ionizable amino acids (Figure 1) through Le Chatelier’s principle. Adding positive hydrogen atoms will make our protein positively charged. So, pH 4 would be a good pH for our buffer if we want to use cation-exchange chromatography.
Alternatively, we could try a basic buffer with pH 10. At pH 10, there will be less hydrogen atoms in solution compared to pH 7 where our protein is neutral. And, due to Le Chatelier’s Principle, the lack of hydrogen ions will lead to deprotonation of our protein’s ionizable groups (Figure 1). Loss of positive hydrogen ions from our protein leads to a negative overall charge. This makes pH 10 a good buffer choice if we are going to use anion-exchange chromatography to purify our protein.
Look at that! By knowing our protein’s isoelectric point and some basic chemical principles we can easily work out which buffer will work well for purifying our protein by ion-exchange chromatography with a couple of quick thought experiments!
Calculating Protein Isoelectric Point
Up to now we have skimmed over where a protein’s isoelectric point comes from. Let’s use a couple of practical examples to demonstrate how protein isoelectric points are calculated, and how you can estimate them.
For the first example, let’s consider the protein “MIKETHECAT”.
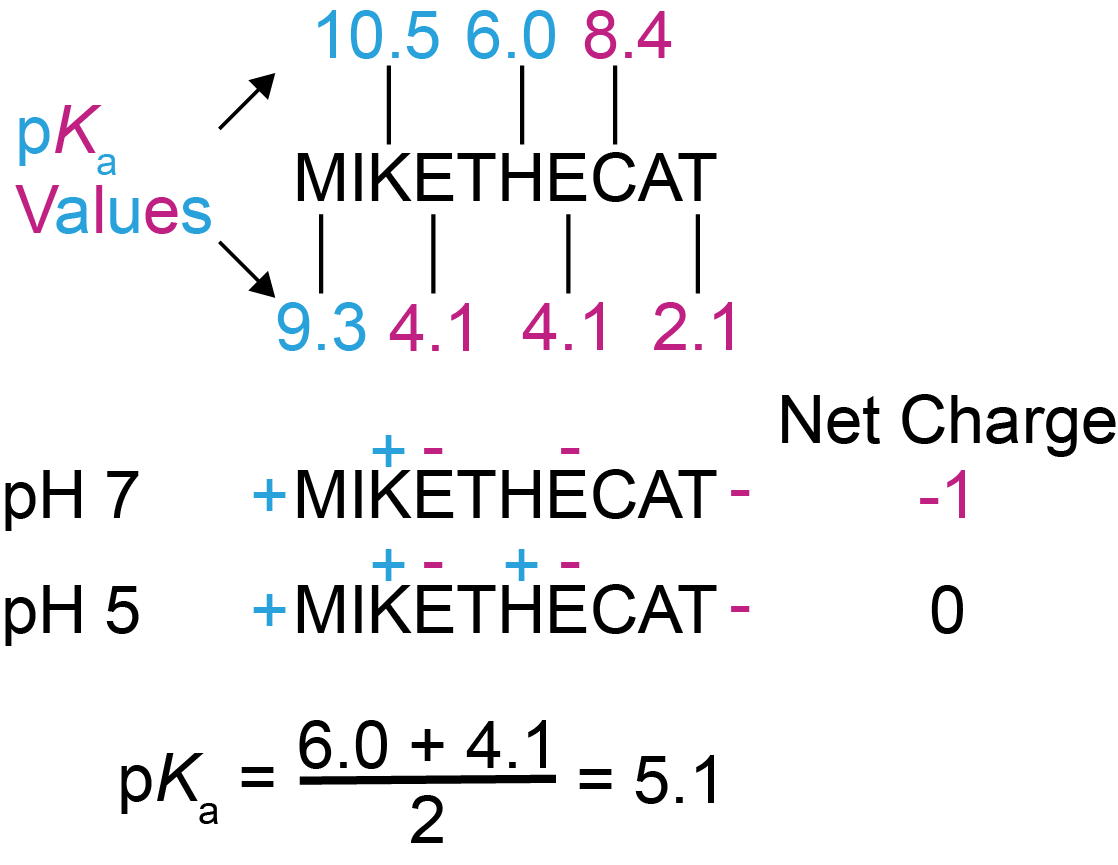
Figure 5.
First example of estimating a protein’s isoelectric point (pI).
First, we need to consider the ionizable groups in this protein sequence. By referring to Table 1, we can find the pKa values for the amino group of M and the carboxy group of T, since they are the first and last amino acids of this protein. We can also look up the side chains for K, E, H, E again, and C – these are the amino acids in this example protein that contain ionizable side chains. The side chains of M, I, T, and A don’t have ionizable groups (Table 1), so they don’t have pKa values and won’t be charged at any pH.
Ok, now let’s guess a pH as a starting point – how about pH 7? At pH 7 the amino terminus and the side chain of K will be positively charged, the carboxy terminus and the side chains of both Es will be negatively charged, and the side chains of H and C will be neutral. That gives the protein a net charge of -1 (Figure 5).
Let’s break down the process in Figure 5 a little bit. First, identify the residues with ionizable side chains from Table 1. Don’t forget the amino and carboxy groups from the first and last amino acids, respectively. Second, find a pH at which the protein is net neutral. Third, find the pKa values in your protein that are just above and below the pH at which your protein is neutral, and average these pKa values to get the estimated pI. That may sound convoluted but follow the examples below and you’ll see it’s actually quite simple.
Recall from our discussion above that to make this protein neutral, we need to make the pH more acidic. By looking at pKa values in Figure 5, we realize that if we change the pH to between 6 and 4.1, this will make the side chain of H positive since the pH will be more acidic than the pKa of H’s side chain (6.0), and not change the charge of any other ionizable group, which will result in a net charge of 0. So now we know that the pI of this protein is close to 5.
To be a little more precise, we average out the pKa values of the ionizable groups just above and below the pH at which the protein is neutral to get a better estimate of the protein’s pI (Equation 5). For this protein, we would average out the side chain pKas for E (4.1), and H (6.0), which gives us an estimated pI of ~ 5.1 (Figure 5).
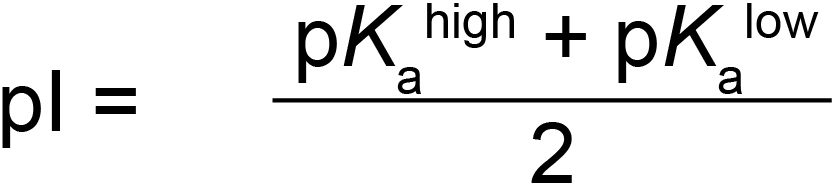
Equation 5. To estimate the isoelectric point (pI) of a protein you average out the pKas of the ionizable groups just above (pKahigh) and just below (pKalow) the pH at which the protein is net neutral.
Let’s work through one more example with the protein “RACHELTHERAT”. Same as before - we look up the pKa values in Table 1, and arbitrarily check the protein’s charge at pH 7. This time we are lucky in that this protein is net neutral at pH 7. So now we average out the proximal pKa values for the side chains of C (8.4) and H (6.0) since they are the pKa values just above and below the pH at which our protein is neutral. Doing this gives an estimated pI of 7.2 (Figure 6).
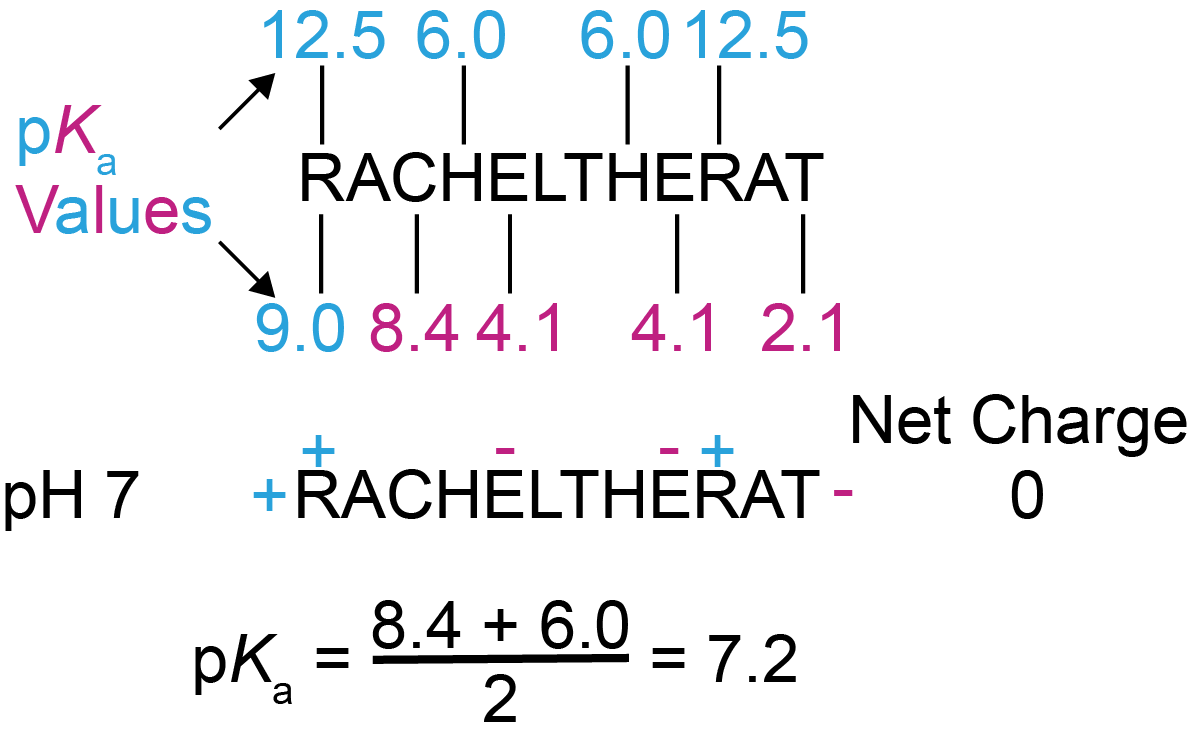
Figure 6.
Second example of estimating a protein’s isoelectric point. Using the same
method as described for Figure 5, we estimate the pI for this protein is 7.2.
Now that we’ve worked through these examples, see Figure 7
for two more proteins that you can work through on your own. After coming up
with your result, go to the end of this article past the References for the
answers and brief explanations.
Figure 7. Try estimating the isoelectric points for these proteins – the answers are at the end of this article past the References.
If you’ve made it this far, I’m pretty sure that you’re now all charged up about protein electrostatics too! Welcome to the club.
References
Rizzo, C. (N.D.). Amino acids. Vanderbilt University. https://www.vanderbilt.edu/AnS/Chemistry/Rizzo/stu...
Answers to Figure 7 Isoelectric Point Estimation
Here are the isoelectric points estimates for the proteins from Figure 7:
#1: pI = 6.7
#2: pI = 8.8
Following the method described above and demonstrated in Figures 5 and 6 will result in these answers. You should note that in this article we are covering the very basics on how to calculate protein isoelectric points. Various pI calculators will use slightly different pKa values and slightly different calculation methods, resulting in slightly different values.
For example, this website is a nice reference for calculating protein isoelectric points. If you look up the proteins in this article, you will see that 16 different values are calculated. These values are all fairly similar, but not exactly the same. For the purposes of ion exchange chromatography don’t worry about these small differences, just make the pH of your buffer at least 1-2 pH units different from most of the calculated values.
.jpg?t=1714409158)
